Pető Lilla: A hálózatelmélet és a közművelődés kapcsolatának elméleti áttekintése
Cikk letöltése: pdf2021-04-06

Absztrakt: Jelen tanulmányban a legdinamikusabban fejlődő tudományterület, a hálózat elmélete és a közművelődés rendszere közötti párhuzamokat igyekszem vizsgálni. Igyekszem párhuzamot vonni a közművelődés és a matematikai hálózatelmélet között és keresni egy utat, amivel feltérképezhető ez a komlex rendszer, melyben tevékenykedünk.
Abstract: In the present study, I try to examine the parallels between the most dynamically developing field of science, network theory and the system of public culture in connection. I try to draw a parallel between public education and mathematical network theory and find a way to map this complex system in which we operate.
A kutatási folyamatot és a tanulmány elkészítését a Nemzeti Művelődési Intézet Közművelődési Tudományos Kutatási Program Tudományos Diákköri munkát végzők számára alprogramja támogatta.
Bevezetés
Jelen tanulmányomban célul tűztem ki, hogy a napjainkban egyre inkább népszerűvé váló hálózatelmélet és hálózatkutatást, amelyet elsőként matematikai és fizikai problémák kapcsán vizsgáltak, a közművelődés viszonyában elemezzem.
A szakirodalom felkutatása kapcsán elsőként Barabási Albert László fizikus e témában alkotott könyveit és tanulmányait tekintettem át (Barabási 1999; 2016), majd általa jutottam el Mark Granovetter szociológushoz (Granovetter 2010), és tértem át az e témában keletkezett társadalomtudományi és hálózattudományi cikkek vizsgálatához.
A könyvek és tanulmányok feldolgozása kapcsán egyértelművé vált számomra, hogy a közművelődés hálózattudományi vizsgálata olyan új módot tud adni a kutatásra, amely mint komplex rendszert képes összehasonlítani a közművelődési intézményeket és színtereket, azok kapcsolatait a közművelődés egyéb szereplőivel. A huszonegyedik században elengedhetetlen a komplex rendszerek vizsgálata, így a közművelődésé is, hiszen számos olyan kapcsolatot, mintázatot lehet felderíteni, amelyekkel az együttműködéseket, az egymáshoz való viszonyokat, az információ áramlását lehet felkutatni. Továbbá a hálózatkutatás segítségével mérhető akár a feladatellátás hatékonysága is. A szakirodalom feldolgozása kapcsán igyekeztem párhuzamot vonni a közművelődés, mint komplex rendszer, és más hálózatok között.
Törvényszerűségek a hálózatelméletben
A hálózatkutatás jelenleg az egyik legdinamikusabban fejlődő tudományterület, világszerte jelennek meg a témában a szakterületről publikációk. Mára szinte nem maradt olyan tudományterület, amely ne alkalmazná ezt a fajta megközelítést (történelemtudomány, szociológia, neveléstudomány, pszichológia, közgazdaságtudomány stb.). A hálózatokat, mint komplex rendszereket, eredetileg a fizika és a matematika alkalmazta először, a fogalmait ezek határozták meg. „A hálózaton olyan rendszert értenek, ahol az egyes alkotó egységek között kölcsönhatás található, melynek következtében a rendszer viselkedése az egyes egységektől eltérő sajátosságokat mutat.” Napjaink egyik legfontosabb feladata a rendszerben való gondolkodás megteremtése, a hálózat alapú gondolkodás. (Rab 2019:39.)
1. ábra: Königsbergi híd probléma
(Forrás: Grund 2018 április 1.)
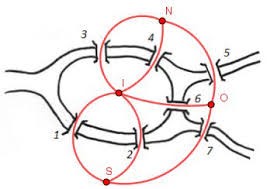
A gráfokról (hálózatokról) való gondolkodás atyja Leonhard Euler svájci matematikus és fizikus, aki egy hétköznapi fejtörő kapcsán alkotta meg azt. „A probléma története, hogy a poroszországi Königsberg (most Kalinyingrád, Oroszország) városban hét híd ívelt át a várost átszelő Prégel folyón úgy, hogy ezek a folyó két szigetét is érintették. A königsbergiek azzal a kérdéssel fordultak Eulerhez, vajon végig lehet-e menni az összes hídon úgy, hogy mindegyiken csak egyszer haladjanak át, és egyúttal visszaérjenek a kiindulópontba. 1736-ban Euler bebizonyította, hogy ez lehetetlen, azaz nem lehet átkelni az összes hídon úgy, hogy mindegyiken csak egyszer haladnak át.” (lásd 1. számú ábra). (Rab 2019: 40.)
A probléma bizonyítása során Euler a helyzetet a gráfelmélet nyelvén fogalmazta meg, azaz leegyszerűsítette azt. A földeket, tehát a folyó partjait, beleértve a szigeteket is, csomópontoknak, a hidakat pedig éleknek tekintette a mai megfogalmazás szerint. Az így létrehozott csomópontok és élek pedig egy gráfot [1] határoznak meg. (Rab 2019: 40.)
A hálózatok vizsgálatánál a kategorizálás és a hálózatok tulajdonságai foglalkoztatták a matematikusokat és a fizikusokat Euler munkája révén. Ám Erdős Pál [2] és Rényi Alfréd[3] megalkották a véletlen gráfok modelljét, amely egy merőben más vizsgálati szempontot jelentett az eddigiekhez képest. A modell lényege, hogy az egyes csomópontok véletlenszerűen kapcsolódnak össze, ezáltal mindegyik egyenrangú, mindnek ugyanannyi esélye van a másikkal való kapcsolatra. (Barabási 2003: 20.)
2. ábra: Erdős-Rényi féle véletlen gráf modell
(Forrás: David Newth: ResearchGate)
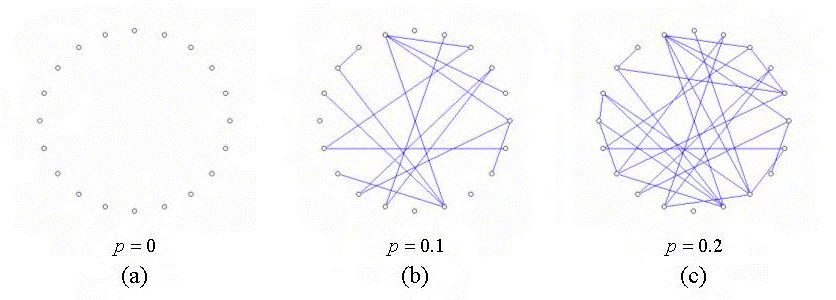
A véletlen gráfok elméletet tovább vizsgálva rájöttek, hogy az egyes pontok között a távolság igen kicsi, bármilyen nagy is az elemszám. Stanley Milgram amerikai szociálpszichológus megalkotta ezen állítás alapján a hat lépés távolság elméletét, amelynek egyik érdekessége, hogy a jelenséggel már 1929-ben Karinthy Frigyes is foglalkozott a Láncszemek [4] című novellájában. Stanley Milgram a teóriát csak 1967-ben bizonyította. „Az amerikai szociálpszichológus az 1960-as években végzett kísérletet az Amerikai Egyesült Államok középnyugati részén. Arra kérte az önkénteseket, hogy saját ismerőseik láncolatán keresztül egy képeslap küldésével találjanak meg egy bostoni ismeretlent. A kísérlet szerint akkor átlagosan öt emberre volt szükség, így hat lépésen át lehetett eljutni egyik embertől bármelyik másikig a világon.” A hat lépés távolság jelenséget, más néven kis világ tulajdonságnak nevezzük. Egy ilyen gráfban a csúcsok közötti átlagos távolság a csúcsok számához képest kicsi. Ez számos hálózatra jellemző, mint például az internetre is. (Barabási 2003: 32-47.)
Az újabb komoly felfedezést a hálózatelméletben Mark Granovetter tette. A gyenge kötések ereje[5] és az A gyenge kötések ereje: a hálózatelmélet felülvizsgálata cikkeiben [6]a hálózatelmélet szociológiai megközelítésével foglalkozott. Első cikkét, amely disszertációjának rövid kivonata, 1973-ban írta, amely az ego, egyén társadalmi hálózatának gyenge kötéseit, azaz távoli ismerősi kapcsolatait vizsgálta a munkakeresési rutinjuk kapcsán. (Rab 2019:47.)
Granovetter állítása szerint a gyenge kötések híd szerepet töltenek be a csomópontok között. Amennyiben egy egyén kevés gyenge kötéssel rendelkezik, úgy a társadalom távoli híreiről nem értesül. „A kommunikációelmélet makroszkopikus oldala az, hogy a gyenge kötések nélküli társadalmi rendszerek széttöredezettekké és inkoherensekké válnak.” (Mark Granovetter 2010: 315.) Barabási Albert László 1999-es kutatásaiban hasonló megállapításra jutott a gyenge kötések kapcsán.
Granovetter szerint a társadalmi rendszerek fejlődésében a gyenge kötéseknek a legfontosabb a szerepük, mert a munkamegosztás, szakosodás és a kölcsönös függés kapcsán létfontosságúvá váltak az egyén számára. Elmélete sok szempontból komoly fordulópontot hozott a hálózatok társadalmi vizsgálata vonatkozásában, mivel addig a gyenge kötéseket nem tekintették fontosnak. Azonban számos területen, így a közművelődés rendszerében is úgy vélem, a gyenge kötéseknek van nagyobb szerepe. (Mark Granovetter 2010: 315.)
A város szociológiai, orvosi, közgazdasági és politikatörténeti kutatások összefoglalóiból két releváns forrást említenék meg a tanulmányában, amelyeket részletesebben is áttekintek.
Az első Fine és Kleinman cikke A szubkultúra újragondolása: egy interakcionista elemzés címet viseli. A szerzőpáros megállapítja, hogy a kulturális eszmék és szimbólumok a társadalom széles metszetén keresztüli gyenge kötések útján terjednek. Továbbá foglalkoznak a kultúra rendszerével is. „Ami azután a kulturális terjesztést lehetővé teszi az, hogy a kultúra megosztására hajlamos összetartó kiscsoportok nem annyira összetartóak, hogy teljesen zártak legyenek, hanem inkább a más hasonló csoportoktól származó eszmék áthatolnak hozzájuk a gyenge kötések közvetítésével… a kultúra gyakorlása választott viselkedésekből áll... A kultúrát lehet stratégiailag alkalmazni és nem szabad úgy felfogni, mint egy feltételes reflexet. A kultúra gyakorlása feltételezi a motivációkat és főként a kulturális témák használóival való azonosulást. Így az értékek, normák, viselkedések és tárgyak csak annyiban alkotnak egy szubkultúrát, amennyiben az egyének egy olyan közösség részének látják magukat, melynek tagjai különleges jelentéseket tulajdonítanak ezen objektumoknak.” (Fine és Kleinman 1972:12-13., Mark Granovetter 2010: 322.) Tehát a kulturális rendszer és eszme kapcsán a fentiek alapján megállapítható, hogy a csoport nem feltétlenül összetartó, azaz inkább a gyenge kötések jellemzik, és nem feltétlen csak azok tartoznak egy csoportba, akiket oda sorolnánk, hanem azok is, akik odatartozónak vallják magukat.
A másik pedig Blau elmélete: „A gyenge kötések túlzott dominanciája, még ha strukturált is, ehelyett egy olyan szituációt hoz létre és tart fenn, amelyikben mindegyik alhálózat nagymértékben átfed sok másikat és a nagyszámú gyenge kötés hídszerű funkciót tölt be.” (Blau1980: 20-21.)
Ezt a megállapítását Blau egy orvosi intézet vizsgálatát illetően hozta, amely intézmény kimondatlan szabálya, hogy baráti kapcsolatok nélkül, laza kapcsolatokkal rendelkezzenek a benne dolgozók. Tehát erős kötések nincsenek a hálózatban, csupán gyenge hídszerű kötések, mégis az intézet kiegyensúlyozottan és jól működik. (Blau1980: 20-22.)
Az Erdős-Rényi féle modellt Granovetter elméletével Duncan Watts szociológus és Steven Strogatz matematikus fogta össze (Strogatz matematikusként Duncan Watts szociológus konzulenseként került kapcsolatba, közös munkájukból számos hálózattudományi munka született). Kutatásukban vizsgálni szerették volna a társadalom csoportfelépítését, ezáltal mérni is azokat, így megalkották a csoporterősségi együtthatót. Ha kiválasztanak egy tetszőleges A és B pontot, akkor hány élen, kapcsolaton keresztül lehet eljutni hozzájuk. Ez a vizsgálat azért érdekes, mert ez adja ki a csoporterősségi együtthatót (tényleges kapcsolatok száma osztva az összes kapcsolattal, ami lehetséges), azaz azt, hogy milyen szoros az összetartása a rendszernek, továbbá ezzel fellelhetőek az összekötő főbb csomópontok is. (Barabási 2003: 53.)
3. ábra: Watts-Strogatz modell
(Forrás: Cornelis J Stam, Jaap C Reijneveld: Nonlinear Biomedical Physics 2007;1: 3)
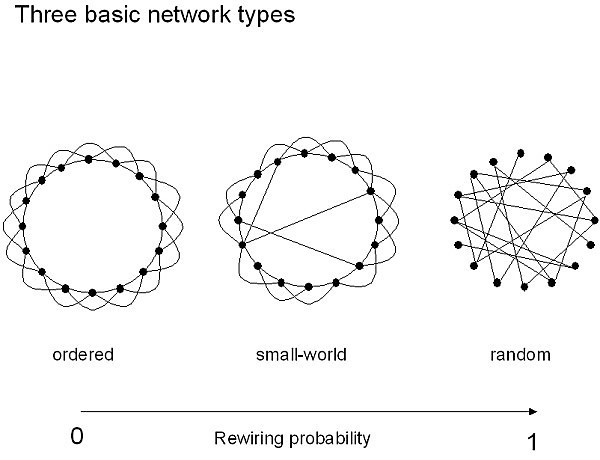
Watts és Strogatz legfontosabb felfedezése ezen vizsgálat kapcsán az volt, hogy a komplex rendszereknek – azaz a hálózatoknak – a csoportképződés fontos és általános tulajdonsága is, amely mindegyikre jellemző. (Rab 2019:48.)
Ez a felfedezés alapjaiban változtatta meg az eddigi hálózatkutatásokat. A szerzőpáros 1988-ban a Nature című folyóiratban publikálta a hálózatok egy újabb modelljét. A csoportképződést újfajta megközelítésből vizsgálták, amelynek lényege, hogy néhány él (kapcsolat) hozzáadásával az egyes pontok közötti távolság nagymértékben csökkenthető, azonban a csoporterősségi együttható nem csökken, változatlan marad. A modell rávilágít arra, hogy a nagy hálózatoknak nem kell minden kapcsolatának véletlennek lennie ahhoz, hogy a kis világ jelenséget mutassák, elég csupán néhány távoli kapcsolattal rendelkezniük. (Barabási 2003: 60-61.)
Barabási Albert László 1999-ben a világhálót tanulmányozta, és arra a megállapításra jutott, hogy vannak olyan hálózatok, amelyekben kiemelkedően magas számú olyan csomópont található, amelyeknek számtalan kapcsolata van. Barabási és kutatócsoportja a komplex kapcsolati rendszereket tovább vizsgálva arra a felfedezésre jutottak ezáltal, hogy bizonyos rendszerekben a középpontokhoz kapcsolódnak újabb pontok, amelyek így létrehozzák a hatványfüggvény eloszlást. (Barabási 2003:63-73.)
Ez a megállapítás nagymértékben különbözik az Erdős-Rényi és a Watts-Strogartz modelltől egyaránt, mellyel a véletlen modell két alapvető törvényszerűségét kérdőjelezte meg. Az egyik, hogy a hálózatban a pontok száma rögzített, a másik, hogy minden pont egyenrangú. (Rab 2019:50.)
4. ábra: Skálafüggetlen hálózat modellje
(Forrás: barabasi.com)
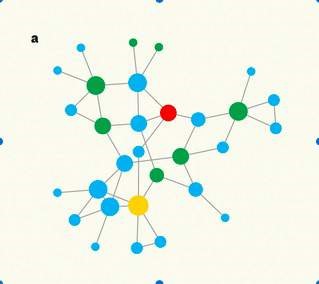
Barabásiék a két feltételezést elhagyva megállapították, hogy a komplex rendszereknek, hálózatoknak saját szabályaik vannak, amelyek szerint működnek, és a szabályok irányítják az egyes pontokat. A kutatócsoport meghatározta, hogy a komplex rendszereket, amelyek a hatványfüggvénnyel leírhatóak, két fő törvény irányítja és mozgatja. Az egyik a növekedés, azaz a folyamatos bővülés. Ezt úgy vizsgálták, hogy egy tetszőleges elemszámú hálózathoz további pontokat adtak, amelyeket véletlenszerűen kötöttek össze. Ám ekkor észlelték a másik fontos szabályt, a népszerűség elérését, ugyanis hiába osztották el véletlenszerűen az egyes pontok kapcsolatait, mégsem lettek egyenértékűek az új pontokkal. Ezt a jelenséget a „gazdag egyre gazdagabb” fordulattal jellemezte Barabási, amelynek lényege, hogy minél régebb óta tagja egy hálózatnak a csomópont, annál több ideje van kapcsolatokat gyűjteni, így az adott csomópont annál nagyobb (népszerűbb). Azaz a „győztes minden visz”, tehát bizonyos csomópontok megszerzik a kapcsolatok legnagyobb részét függetlenül attól, hogy mekkora a rendszer. Az ez alapján felállított hálózat skálafüggetlen modell néven vált ismertté. (Barabási 2003: 90-105.)
A „győztes mindent visz”, és a „gazdag egyre gazdagabb” elmélet határozza meg a kutatócsoport szerint leginkább az ezen törvények által létrehozott rendszert. A fizikusok és matematikusok a szabályok kapcsán vizsgálják a rendszer stabilitását is az alapján, hogy vajon hány pontot kell eltávolítani ahhoz, hogy egy hálózat darabjaira essen, mennyi csomópontot (összekötőt) kell eltávolítani, hogy széttöredezzen a hálózat. Ez a stabilitási vizsgálat megmutathatja, hogyha bizonyos csomópontot vagy összekötőt eltávolítunk, annak milyen hatása lehet a hálózat egészére. (Barabási 2003: 98-105.)
A további kutatások alapján a hálózattudománnyal foglalkozó fizikusok és matematikusok meghatározták a pontoknak egy újabb típusát (egyszerű pontok, csomópontok), azokat a középpontokat, akiket újítóknak neveztek el. Az újítók a hálózat befolyásolására, a döntések irányítására alkalmas pontok. (Barabási 2003: 123.)
Vizsgálják a kutatók továbbá a hálózatok modularitását is, amelynek lényege, hogy egy csomópont melletti két szomszédos pontot elemeznek akként, hogy mennyire vannak összekötve egymással, hány szállal kapcsolódnak egymáshoz. Amennyiben a modularitás vizsgálatánál hierarchiát fedeznek fel, úgy azon rendszer egymástól külön is képes fejlődni. (Barabási 2003: 216-235.)
A matematikusok és fizikusok mellett számtalan társadalomtudós is foglalkozott a hálózatelmélettel (pl. Granovetter). Magyarországon Szántó Zoltán az, aki a társadalmi hálózatokat vizsgálja kollégáival. Munkái közül a számomra legmeghatározóbb cikkét emelném ki a témában. Szántó Zoltán és Tóth István György A társadalmi hálózatok elemzése című[7] munkájukban a szociológia hálózatelméleti vizsgálatának lehetőségével, módszertanával foglalkoznak. A hálózatelemzés elméleti előzményei szerintük a szociometria néven ismertté vált szociálpszichológiai elemzések. A szociometria vizsgálatok az emberi kapcsolatok mérésével foglalkoznak a társadalmi szerkezet és jólét összefüggésében. Emellett előzménye a hálózatelmélet vizsgálatának a triád- kapcsolatok is, amik a társadalom geometriájának megalkotásában, a társadalmi kapcsolatok módszeres leírásával foglalkozik. Lényege, hogy kölcsönhatásokat vizsgálnak az egyes pontok között, tehát a konfliktusokat, együttműködéseket és az alá-fölé rendelt kapcsolatokat határozzák meg vele a tudósok. (Szántó – Tóth 1993: 32-35.)
Az egyik legfontosabb eredménye a cikknek, hogy a hálózatok jellemzőit társadalomtudományi szempontból határozza meg, ezek alapján beszélünk:
- alanyokról – pontok/csomópontok
- viszonyokról – élek/ kapcsolatok, kötődések (Szántó – Tóth 1993: 36.)
Szántó Zoltán és Tóth István György állítják, hogy a pontokat a viszonyok által összekötve hálózatnak tekintjük, és amennyiben ezen viszonyok típusai többféleképpen rendezhetőek, többféle halmazba sorolhatók, akkor többrétegű hálózatról beszélünk. Ez fontos fordulópont volt számomra, mert én is arra hajlok, hogy minden bizonnyal a vizsgált téma kapcsán is egy többrétegű hálózatról beszélhetünk, hiszen a Nemzeti Művelődési Intézet megyei igazgatóságai külön alrésze a közművelődés hálózatának, de a közművelődéssel foglalkozó civil szervezetek is. (Szántó –Tóth 1993: 42-45.)
A viszonyok kapcsán további fontos megállapítást a cikkben, miszerint „A kapcsolatok különbözhetnek egymástól a kapcsolatok irányítottsága szerint. Ebből a szempontból a hálózati kapcsolatok lehetnek irányítás nélküliek vagy irányítottak, ez utóbbiak pedig szimmetrikus vagy aszimmetrikus irányultságúak. A rokonszenvi-ellenszenvi választások esetén könnyen előfordulhat, hogy az egyik egyén választja a másikat anélkül, hogy választása viszonzásra találna.” (Szántó –Tóth 1993: 37.)
A tanulmány emellett számba veszi azokat a fontosabb mutatókat, amelyeket érdemes vizsgálni egy ilyen típusú kutatásnál:
- „hálózati pont foka, kapcsolatainak száma
- kapcsolatainak iránya alapján
- kimenő
- bejövő
- multiplexitás – kapcsolatok rétegzettsége
- rétegzettségi index
- sűrűség – egymáshoz kapcsolt pontok sűrűsége
- elérhetősége – mennyire jól lehet megközelíteni a többihez képest egy adott egyént/pontot
- centrális szereplők száma
- elszigeteltek száma
- presztízs vizsgálat, amennyiben hierarchikus egy hálózat, úgy a fogadott kapcsolatok alapján vizsgálandó
- kohéziós erő/kölcsönös választások mennyisége” (Szántó –Tóth 1993:42-43.)
A közművelődés rendszere
Az alábbi fejezetben áttekintem a közművelődés rendszerének kialakulását, amelyet négy nagyobb történeti egységre bontottam. Ebben Sári Mihály által felvázolt közművelődési intézményrendszer tipológiáját használtam fel, és egészítettem ki. Sári az alábbi korszakokat határozta meg:
„1. Átmenet az agrártársadalomból az ipari társadalomba (feudalizmusból a polgári társadalomba) a XVIII. század utolsó harmadától a XX. század elejéig
2. Az intézményesült szervezetek korszaka (1920-1949)
3. A szocialista intézményrendszer és professzionalizmus korszaka (1949-1989)
4. Az 1989-től kezdődött rendszerváltás és új terméke: a művelődési otthonok negyedik generációja” (Sári 2004: 102.)
A művelődés egyidős az emberiséggel, hiszen mindig is az emberi élet mozgatója volt a tudás megszerzése. A reformációig a katolikus egyház volt a fő mozgatója a műveltség terjesztésének és a királyi udvarok. Ahol az írnokok és tudósok által elsajátított képességek terjesztődnek a kulturális hálózatban. (Juhász 2016: 17.)
A reformkorban a polgárosodás folyamatának eredményeképpen létrejöttek az egyletek, kaszinók és a nemzeti intézetek, amelyeknek elsődleges célja volt az ismeretterjesztés, a felnőtt nevelés. Az újonnan létrejött intézmények és szervezetek elősegítették a szélesebb társadalmi rétegek művelődését. A nagy központi egyletekhez, mint a Kossuth Lajos nevéhez fűződő Magyar Iparegylethez vagy a Nemzeti Casinóhoz is számos vidéki „fiókegylet” csatlakozott. Véleményem szerint ez a folyamat is a korai kulturális hálózatosodás irányába mutatott. (Juhász 2016: 23.) Ebben az időszakban jöttek létre az olvasóegyletek, olvasókörök, társalgási egyletek is, amelyek a hálózat további bővülését eredményezték. (Maróti 1998:125-126.)
Az 1848-49-es szabadságharc leverésével a fejlődés bizonyos szempontból megtorpant, nyíltan nem lehetett folytatni azt a folyamatot, amit a polgárosodás érdekében elindítottak. Azonban a hálózat létrejötte elősegítette azt, hogy a művelődés ne torpanjon meg teljesen. Az olvasókörök voltak talán ebből a szempontból a hálózat legfontosabb csomópontjai, hiszen a folyóiratok és könyvek terjesztésében kiemelkedő szerepük volt, és a hatalom sem tartotta „kártékonynak” a többi egylethez képest, így a kulturális rendszer viszonylagos stabilitással tudta megőrizni az eddig kialakult hálózatát. (Juhász 2016: 25.)
1882-ben Odeschalchi Gyula országgyűlési képviselő szervezésével elindult a Felvidéki Magyar Közművelődési Egylet, amelynek elsődleges célja volt a felvidéki lakosság magyarosítása. (Juhász 2016: 27.) A dualizmus korszakának második felében egyre több közművelődéssel foglalkozó egylet alakult meg, mellyel elkezdődött a hálózat további kiépülése. Azonban ez a fajta hálózatosodás nem bizonyult teljes mértékben hatékonynak, mert a leginkább érintett rétegekhez nem tudott az információ, a népművelés eljutni. Ezért már az 1890-es években úgy gondolták, hogy fontos, hogy az állam támogassa a folyamatot szellemiségében és anyagilag is egyaránt. Ennek eredményeképp az 1900-as években újabb lendületet kapott a népművelési célú egyletek létrejötte, a hálózat így tovább növekedhetett. 1914-ben Baján Bellosits Bálint létrehozta az első népfőiskolát, amely intézmény még a mai napig is a közművelődési intézményrendszer és a felnőttkori tanulás fontos elemének tekinthető. (Juhász 2016: 32.)
A két világháború között Klebersberg Kunó és Hóman Bálint munkásságának köszönhetően létrejöttek a népházak, művelődési házak. A céljuk az volt, hogy minden településen működjenek népházak, hogy a társadalom legszélesebb rétegét tudják elérni és tanítani. A népházak mellett a népfőiskolák száma is gyarapodott: az 1920-as évekre közel 70 népfőiskola működött. Ennek az emelkedésnek köszönhetően a közművelődési intézményrendszer olyan léptékű fejlődésnek indult, amelyre korábban nem volt példa. Természetesen a népfőiskolák és népházak hálózatként működtek, tudtak egymás munkásságáról, jó gyakorlataikról közösen tanácskoztak, ellátogattak egymáshoz, igazi hálózatként funkcionáltak. (Juhász 2016: 33.) A szakirodalom ezt a korszakot az intézményesített szervezetek korszakának tekinti: a művelődési otthonok második generációja jött létre, amelyek helyt adtak a tudományos előadásoknak, tanfolyamoknak és különféle szórakoztató rendezvényeknek. (Sári 2001: 47.)
A második világháború után a közművelődés, népművelődés erős állami befolyás alá került. Felszámolták az egyesületeket, népfőiskolákat és a civil szektort. Összességében elmondható, hogy államosítás alá került a kultúra és az oktatás is. A szervesen alulról létrejövő egyleteket, népházakat, népfőiskolákat vagy beszüntették, vagy államosították, ezáltal beleavatkozott a rendszer a hálózat addigi struktúrájába. Létrejöttek a művelődés új intézményegységei, az úgynevezett szocialista művelődési otthonok, melyeknek fő feladata volt, hogy a szocialista ideológia mindenhova eljusson, és szórakoztasson. (Sári 2004:104.)
Csakhogy a változások nem ingatták meg annyira a közművelődés alulról építkező rendszerét, hogy a megszűnjön: létrejöttek különféle klubok és közművelődési társulások, amelyek lényege az volt a hálózat szempontjából, hogy a betiltott vagy a megszűnt csomópontok helyére újak kerültek. Azonban volt még egy fontos mozzanata a korszaknak: 1956-ban elindult a népművelés szakos képzés, elsőként Debrecenben Durkó Mátyás nevéhez kötődően, majd Budapesten Maróti Andorhoz kapcsolódóan. (Juhász 2016: 40.)
Emellett az akkori közművelődési koncepció és közművelődési törvény, amely mindenkor a hálózat működését segítette elő, széles szakmai kör bevonásával került megvitatásra, a törvény által biztosították az intézményi rendszer finanszírozását is. (Juhász 2016: 41.)
A képzésnek köszönhetően a szakemberek felkészítése biztosított volt, a közművelődési törvény által az anyagi forrás is rendelkezésre állt, így a közművelődés intézményrendszere stabilizálódni tudott. Újabb intézménytípus is létrejött (Általános Művelődési Központ) még inkább kiszélesítve a csomópontok rendszerét. (Juhász 2016: 42.)
A rendszerváltás előtt létrejövő kulturális törvény (1976.V.sz), amely alapvetően határozta meg az állam és a közművelődés viszonyát, csak 1997-ben került hatályon kívül, amikor az Országgyűlés megszavazta a muzeális intézményekről, a nyilvános könyvtári ellátásról és a közművelődésről szóló 1997. évi CXL törvényt. Az új jogszabály meghatározta az állami és önkormányzati szerepvállalás és felelősségvállalás mértékét és a közművelődési intézmények tulajdonosait. 2012-ben újabb módosításra került sor a 2012. évi CLII. törvény életbelépésével, mellyel a muzeális intézményeket és kulturális javakat szilárdították meg. Emellett megszűntek a közművelődési központok és helyettük kulturális központok jöttek létre. Az intézményi rendszert tovább tisztázta az 1997-es ágazati törvény módosítása.
A 2017. évi LXVII törvénnyel módosított ágazati jogszabály értelmében deklarálásra került a kulturális alapellátás („A kulturális alapellátás célja, hogy mindenki számára elérhető kultúrát közvetítsen, egyéneket és közösségeket aktivizáljon. Települési szinten kerülhessen megfogalmazásra, milyen értékek, célok és fejlesztési irányok az elsődlegesek, helyben legyen lehetőség a közösségi élet fejlesztésére, mindehhez szakmai segítséget és állandó helyszínt ad a közművelődési szakma.”). (Kary et al. 2018:7.) Ennek következtében egy olyan rendszer alakult ki, amely tisztázza az alapszolgáltatások körét, meghatározza a feladatellátók típusait, és az egyes típusok mellé személyi, tárgyi feltételeket és szolgáltatásokat rendel hozzá.
A közművelődési alapszolgáltatások:
„a) művelődő közösségek létrejöttének elősegítése, működésük támogatása, fejlődésük segítése, a közművelődési tevékenységek és a művelődő közösségek számára helyszín biztosítása;
b) a közösségi és társadalmi részvétel fejlesztése;
c) az egész életre kiterjedő tanulás feltételeinek biztosítása;
d) a hagyományos közösségi kulturális értékek átörökítése, feltételeinek biztosítása;
e) az amatőr alkotó- és előadó-művészeti tevékenység feltételeinek biztosítása;
f) a tehetséggondozás- és fejlesztés feltételeinek biztosítása;
g) a kulturális alapú gazdaságfejlesztés” (1997. évi CXL. törvény 76.§ (3) bekezdés)
A közművelődési intézmény lehet:
„a) művelődési ház,
b) művelődési központ,
c) kulturális központ,
d) többfunkciós közművelődési intézmény,
f) népi kézműves alkotóház,
g) gyermek-, illetve ifjúsági ház, valamint
h) szabadidőközpont.” (1997. évi CXL. törvény 77.§ (5) bekezdés)
Az alapszolgáltatások rendszerét és a közművelődési intézmények személyi tárgyi feltételét a 20/2018. (VII.9.) EMMI rendelet foglalja össze. (Oszlánczi 2019:129)
„Napjainkban a közművelődési szakma megújítása zajlik: a szakma új felsőoktatási szakokat indított, új intézménytípusokat vezetett be, tartalmi, személyi és infrastrukturális feltételeket határozott meg, és előírták a különböző munkakörökhöz szükséges képzettségi feltételeket is. A változások minden település életében új lehetőségeket teremtettek, szemléletbeli változásokat idéztek elő.” (Závogyán Magdolna et al.2019.)
Ahogy a korábban is, most is megállapítható, hogy a törvényi változás mindig a hálózat stabilitását hozza magával, hiszen a rendszert alkotó csomópontok tisztázódnak feladatkörükben és az egymás közti viszonyukban egyaránt.
Fontos emellett megemlíteni, hogy a törvényi változások mellett a társadalmi folyamatok is alakítják társadalmunkat, így a közművelődés rendszerét. Ennek a változásnak a legjobb bizonyítéka az Euroicities nemzetközi hálózattal rendelkező szervezet stratégiájában található. Anyagukban öt fejlesztési tényezőre hívják fel a figyelmet, amelyek közül számomra a három legfontosabbat emelném ki. A közművelődés hálózatát is nagyban befolyásolják a demográfiai változások: az elmúlt 100 év alatt a lakosság korcsoportja átalakult. Az elmúlt évszázad első felében még a 20 év alatti korcsoport tette ki a lakosság legnagyobb részét, ez az arány mára a felére csökkent, viszont a 60 év feletti korcsoport megoszlása megduplázódott. (Juhász 2018:48.) A második kihívás, amivel számolni kell a hálózatnak, az a digitális kihívás, amely a pandémia miatt még inkább felerősödött, és a kultúra területét éppúgy érinti, így a közművelődést is. Véleményem szerint a hálózat egyes pontjainak a megmaradása és a közösség megőrzésének alapvető eleme a digitális rendszerekben rejlik, az online jelenlétben.
5. ábra: Öt kulcskihívás a kultúrában
(Forrás: Juhász 2018:47)
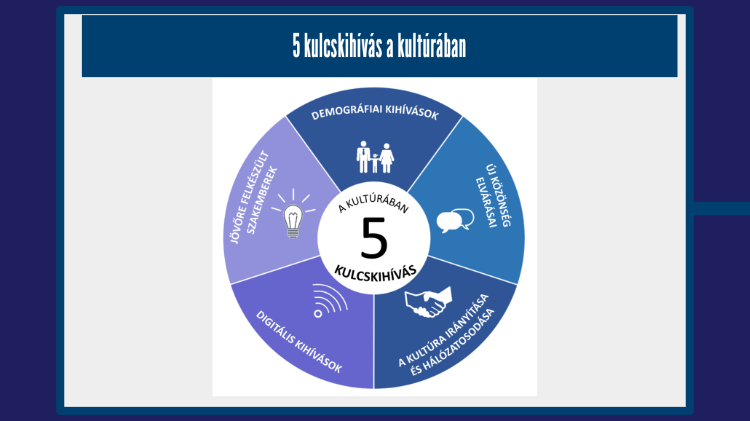
Ezen öt kihívásból pedig a legfontosabb a hálózatosodás a kultúrában. A közművelődési intézmények feltételezésem szerint egy hálózatot alkotnak, szervesen kapcsolódnak egymáshoz, mellyel komoly társadalmi szerepet töltenek be. (Juhász 2018:48, Svidró 2019: 116.)
Összegző megállapítások a hálózatelmélet és a közművelődés rendszere kapcsán
A hálózatelméleti áttekintés számomra bizonyosságot adott, hogy a közművelődés, mint komplex rendszer hálózatnak tekinthető, megtalálhatóak benne azok a tulajdonságok, amelyek a hálózatokat jellemzik.
Granovetter elmélete sok szempontból komoly fordulópontot hozott a hálózatok társadalmi vizsgálata kapcsán, mivel addig a gyenge kötéseket nem tekintették fontosnak. A közművelődés szemüvegén át nézve érdekes vizsgálati kiindulópontot ad ahhoz, hogy kutassuk, vajon a hálózatunkban az önkéntes gyenge kötések, vagy az erős kötések, melyek a szerződések kapcsán jönnek létre – agóra feladatellátási szerződése – határozzák meg jobban rendszerünket, mennyire fontosak az erős kötések a mi rendszerünkben, vagy mennyire lényegtelenek azok. Szerintem a társadalmi rendszereket, mint ahova a közművelődést is sorolom, sokkal inkább a gyenge kötések, a laza kapcsolatok jellemzik jobban.
A kultúra és gyenge kötések kapcsolata a közművelődés szempontjából fontos bizonyítékot és relevanciát mutatnak a hálózati működésnek és a kultúra terjesztésének, közművelődési feladatának vizsgálatára.
Számomra jelen tanulmány kapcsán a legfontosabb megállapítás Barabási kutatásaiban az, hogy a komplex rendszereknek, hálózatoknak saját szabályaik vannak, amelyek szerint működnek, a szabályok irányítják az egyes pontokat. Ez a tulajdonság, amely jellemzi a hálózatokat, számomra rögtön a közművelődés szabályrendszerét juttatta eszembe: az 1997. évi CXL. törvényt és a hozzá kapcsolódó 20/2018 (VII.9) EMMI rendeletet (végrehajtási rendelet), amely a legalapvetőbb feladatokat, elvárásokat, személyi és tárgyi feltételeket tartalmazza, amit jelen esetben is a hálózat szabályának tekinthetünk. (Barabási 2003: 7-14.)
Egy hálózatban, ha véletlenül választunk ki és kötünk össze pontpárokat, akkor bizonyos szintű közösségi kapcsolat alakul ki. Ez a folyamat a közművelődés rendszerére is abszolút releváns állításként vehető át. A pontokat és éleket, amelyek a hálózatot alkotják, a közművelődés nyelvére fordítva úgy képzelem, hogy a pontok a közművelődési intézményeknek és színtereknek, illetve egyéb szervezeteknek, köztük a Nemzeti Művelődési Intézet megyei „hálózatának” részei. Az élek pedig, amik összekötik a pontokat nem mások, mint a kapcsolatok, amelyek lehetnek önkéntesek, vagy kötelezőek. Önkéntesnek azokat a kapcsolatokat tekintem a közművelődés rendszerében, amelyben nem formális módon történik az együttműködés, kötelezőnek pedig azokat a kapcsolatokat, amelyekben valamilyen szinten szerződéses megállapodás jön létre, például egy agóra feladatellátási szerződése kapcsán. (Barabási 2003: 15-31.)
Vizsgálják a fizikusok továbbá azt is, hogy egy pontnak mennyi kapcsolata van, a pontok között milyen erős kötés van (megkülönböztetnek gyenge és erős kötéseket). A közművelődés, mint komplex rendszer – ha pusztán a hálózatelmélet alapján kerül górcső alá és modellezzük le – akkor mennyire erős, van-e olyan pont, ami elszigetelődik, hol van a közművelődés vakfoltja. (Barabási 2003: 63-73.)
A stabilitási vizsgálat hasznos lehet a közművelődés hálózatának vizsgálatában is, ugyanis megmutathatja, hogyha bizonyos csomóponti vagy összekötő intézményeket eltávolítunk, annak milyen hatása lehet a hálózat egészére. Ezzel szerintem igazolható lehet egy adott intézmény létjogosultságának empirikus bizonyítása. (Barabási 2003: 98-105.)
Az újítók a hálózat befolyásolására, a döntések irányítására alkalmas pontok. Vajon a közművelődésben vannak ilyen pontok? Kettő minden bizonnyal van, amennyiben a rendszer részének tekintjük. Ez az újító pedig a mindenkori minisztérium és a Nemzeti Művelődési Intézet, hiszen a szabályok és döntések a minisztériumból érkeznek és a mintaprogramok és módszertani anyagok, a közművelődés kánona pedig a Nemzeti Művelődési Intézet országos feladatköréből származik. (Barabási 2003: 123.)
A közművelődés történeti kialakulásának vizsgálata bizonyosságot adott arra, hogy valóban egy szervesen fejlődő komplex rendszerrel állunk szemben, amely hálózatnak tekinthető. A rendszer főbb csomópontjai az évszázadok alatt folyamatosan alakultak át, növekedtek, a kapcsolódásaikat a mindenkori rendszer formálta.
A kulturális törvények általi intézményesülés pedig folyamatosan erősítette a rendszert. A jogszabályok alakították a hálózatunkat, tisztázták a csomópontokat (közművelődési intézmények és közösségi színtér beazonosításával), feladatokat, személyi és tárgyi feltételeket határoztak meg.
A közművelődés történelmi távlatból nézve is a kapcsolati hálózaton keresztül tudott alakulni, fejlődni, híd szerepet töltöttek be az egyletek és számos újító jellemzi azt.
Az Eurocities stratégiájában foglaltak szintén megerősítést adtak abban, hogy a kultúra hálózatosodása, mint kulcskihívás mennyire fontos jelen korunkban. Nemcsak általam képviselt megállapításról van szó, ennek a fontosságát adja a többi négy kulcskihívásra adott válasz is, amely véleményem szerint a hálózati gondolkodással, a rendszerelmélettel oldható fel.
Felhasznált irodalom:
- 1997. évi CXL. törvény a muzeális intézményekről, a nyilvános könyvtári ellátásról és a közművelődésről. (elérhető: https://net.jogtar.hu/jogszabaly?docid=99700140.tv, letöltés dátuma: 2020.12.15)
- 2017. évi LXVII. törvény a muzeális intézményekről, a nyilvános könyvtári ellátásról és a közművelődésről szóló 1997. évi CXL. törvény és egyes kapcsolódó törvények módosításáról
- 20/2018. (VII. 9.) EMMI rendelet a közművelődési alapszolgáltatások, valamint a közművelődési intézmények és a közösségi színterek követelményeiről.
- Barabási, Albert László (2003): Behálózva, Libri Könyvkiadó
- Barabási, Albert László (2016): A hálózatok tudománya, Libri Könyvkiadó
- Durkó, Mátyás – Sári, Mihály (1990): A népművelés és a felnőttnevelés történeti fejlődésének vázlata. In: Durkó, Mátyás – Sári, Mihály: Bevezetés a közművelődéselméleti ismeretekbe. Budapest, Tankönyvkiadó.
- Granovetter, Mark (1973): The Strength of Weak Ties in American Journal of Sociology Vol. 78, No. 6 (May, 1973), pp. 1360-1380
- Juhász, Erika (2016): A felnőttek képzése és művelődése egykor és ma Magyarországon. Debrecen, Csokonai Kiadó
- Juhász, Erika (2018): Kultúra és tőke: befektetés a közösségi művelődésbe. In: SZÍN 23. évfolyam 3. szám pp.47-50. p (elérhető: http://epa.oszk.hu/01300/01306/00152/pdf/EPA01306_szin_2018_3_47-50.pdf., letöltés dátuma: 2021.01.26)
- Kary, József et al. (2018): Útmutató a közművelődési szakterület megújult jogszabályi környezetének alkalmazásához. Budapest, NMI Művelődési Intézet Nonprofit Közhasznú Kft.
- OSAP 1438 – Közművelődési statisztikai adatok 2019-es évről
- Maróti, Andor (1998): Fogalomváltás a magyar népművelés és felnőttoktatás történetében. In: Maróti, Andor – Rubovszky, Kálmán – Sári, Mihály (szerk.): A magyar felnőttoktatás története. [Felnőttoktatás, továbbképzés és élethosszig tartó tanulás sorozat 18. kötet] Budapest, Magyar Művelődési Intézet – Debreceni Kossuth Lajos Tudományegyetem Művelődéstudományi és Felnőttnevelési Tanszéke – Jászberényi Tanítóképző Főiskola Közművelődési és Felnőttnevelési Tanszéke – Német Népfőiskolai Szövetség Nemzetközi Együttműködési Intézete Budapesti Projektirodája. 125-126.p.
- Oszlánczi, Tímea (2019): A közművelődés jogszabályi változásainak fő irányvonalai. In: Virág, Irén (szerk.): Az Eszterházy Károly Egyetem tudományos közleményei – Tanulmányok a neveléstudomány köréből. [Acta Universitas, Sectio Paedagogica], Eger. 127-129. p. (elérhető: http://publikacio.uni-eszterhazy.hu/4631/1/125_133_Oszl%C3%A1nczi.pdf letöltés dátuma: 2021.03.01.)
- Rab, Virág (2019): A kapcsolati hálózatok a történelemben, Gondolat kiadó
- Sári, Mihály (2004): A kultúra intézményrendszereinek történeti-funkcionális változásai. Pécs, PTE FEEFI
- Svidró, Ibolya (2019): Kulturális állapotfelmérés a közművelődési intézményrendszerben. In: Kulturális Szemle 12. szám 111-120.p.
- Szántó, Zoltán – Tóth, István György, (1993): A társadalmi hálózatok elemzése in: Aula Vol. 15, No. 1 (1993), pp. 30-55
- Závogyán, Magdolna et al. (szerk.) (2019): Útmutató II. a közművelődési feladatellátás dokumentumainak elkészítéséhez – Példatár. Lakitelek, Nemzeti Művelődési Intézet.
[1] „Gráfnak nevezzük pontoknak és éleknek a halmazát, ahol az élek pontokat kötnek össze, illetve az élekre pontok illeszkednek úgy, hogy minden élre legalább egy, legfeljebb két pont illeszkedik.” (Forrás:https://tudasbazis.sulinet.hu/hu/matematika/matematika/matematika-11-osztaly/bevezetes/grafelmeleti-alapfogalmak-tetelek) (Letöltés ideje: 2021.02.16)
[2] „1913 -1996 ErdősPál, a világhírű matematikus, a magyar matematika, a modern kombinatorika és gráfelmélet egyik legmeghatározóbb alakja.” forrás:http://www.matud.iif.hu/2013/11/12.htm (letöltés ideje 2020.11.19)
[3] „Rényi Alfréd (1921-1970) Tudományos munkássága lefedi a matematika majdnem valamennyi ágát, sok területen alkotott maradandót. Kombinatorikában az ő nevéhez (is) fűződik az első véletlen gráfmodell, az úgy nevezett Erdős-Rényi véletlen gráf definiálása és az első néhány ehhez kapcsolódó tétel bizonyítása.” (Forrás:https://www.renyi.hu/hu/intezeti-bemutatkozas-hu/az-intezet-tortenete/renyi-alfred) (Letöltés ideje: 2020.11.19)
[4] A novella elérhető: http://mek.niif.hu/07300/07367/html/01.htm#54
[5] A cikk elérhető: https://www.jstor.org/register?redirectUri=%2fstable%2f10.2307%2F2776392%3Fread-now%3D1%23page_scan_tab_contents&refreqid=excelsior%3Af2fd0b2aac8ce414b7f4903b304e7c32 (Letöltés ideje: 2020.04.13)
[6] A cikk elérhető: https://regi.tankonyvtar.hu/hu/tartalom/tamop425/0010_2A_19_Tarsadalmi_retegzodes_olvasokonyv_szerk_Gecser_Otto/ch06s03.html#ftn.id585688 (Letöltés ideje: 2020.04.13)
[7] http://www.socialnetwork.hu/cikkek/szanto_toth_cikk.pdf (Letöltés ideje: 2020.03.16)
